Сумма внутренних углов любого четырехугольника составляет 360 градусов. Это фундаментальное свойство евклидовой геометрии, которое справедливо для всех типов четырехугольников, включая квадраты, прямоугольники, параллелограммы, трапеции и произвольные четырехугольники.
Содержание
Доказательство суммы углов четырехугольника
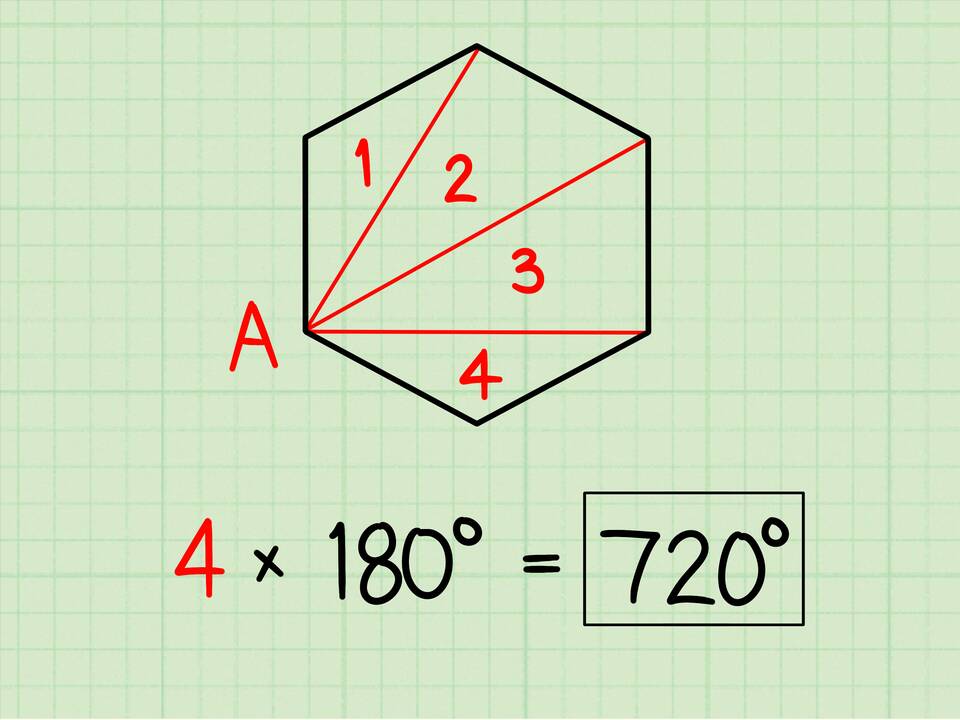
Четырехугольник можно разделить диагональю на два треугольника. Поскольку сумма углов каждого треугольника равна 180 градусам, общая сумма углов четырехугольника составляет:
- 180° (первый треугольник) + 180° (второй треугольник) = 360°
Примеры для различных четырехугольников
| Тип четырехугольника | Углы | Сумма углов |
| Квадрат | 90° + 90° + 90° + 90° | 360° |
| Прямоугольник | 90° + 90° + 90° + 90° | 360° |
| Ромб | 60° + 120° + 60° + 120° | 360° |
| Произвольный четырехугольник | 80° + 110° + 70° + 100° | 360° |
Сумма внешних углов четырехугольника
Для любого выпуклого четырехугольника сумма внешних углов (по одному при каждой вершине) также равна 360 градусам, как и для других выпуклых многоугольников.
Практическое применение
Знание суммы углов четырехугольника используется в архитектуре, инженерии, компьютерной графике и при решении геометрических задач. Это свойство позволяет вычислять неизвестные углы четырехугольника, если известны остальные.